These are important concepts but tend to be shrouded in confusion. Here's to grasping what it is all about.
Step I: Understand borrowing and lending.
A company or financial institution may need money to expand their business, build a new plant, purchase machinery, buy new land or acquire another company.
One of the ways to raise money is to issue bonds.
Let’s examine this. On February 28, 2020, HMEL issued bonds of Rs 10 lakh each with a 10-year maturity, and a coupon of 9.18%.
- Face Value, or Par Value: The FV is the value assigned to the bond. This is the amount of money loaned to the issuer and it will be returned to the lender on maturity. This is static. In this example is Rs 10 lakh.
- Maturity: This is the length of time of the financial contract. In this case, it is 10 years. So the investor who bought a bond would be loaning HMEL Rs 10 lakh for a period of 10 years.
- Coupon Rate: Now the investor needs to get compensated for lending his money. The CR is the annual rate of interest that could be paid semi-annually or annually. This is static, in the sense that it is fixed when the bond is issued. In this example it is 9.18% of Rs 10 lakh every year, over 10 years.
So what happened here?
When you buy a bond, you lend money to the company that issued the bond (issuer). In exchange, the company makes a legal commitment to return your money (principal) on a predetermined date (maturity date), and till it does so, it will pay you a specified rate of interest (coupon rate) on predetermined dates.
Whether the company makes profits or incurs losses, or its stock price rises or falls, that is irrelevant to the terms and conditions. It still has to pay the coupon rate promised and return the principal on the specified date.
Step II: Understand Yield.
During these 10 years, the bond will be traded in the market. As with any instrument traded, the price will rise or fall. As that happens, the market price of the bond will differ from the Face Value (FV). But since the Coupon Rate (CR) is static, and is a percentage of FV, the return will differ. This return is called yield.
Let’s work it out.
- FV = Rs 100
- CR = 5% p.a
- Amount investor earns every year = Rs 5 (5% of Rs 100 is Rs 5)
In the market, the price rises to Rs 110. A buyer is paying more than the FV of Rs 100. However, return is still Rs 5 per annum. Rs 5 on Rs 110 = 4.55%. So the bond yield has fallen because the bond price has risen.
In the market, the price falls to Rs 90. A buyer is paying less than the FV of Rs 100. However, return is still Rs 5 per annum. Rs 5 on Rs 90 = 5.55%. So the bond yield has risen because the bond price has fallen.
Did you get it?
Yield is the return you get by applying the CR to its market price. It is the return you will get when you buy the bond at that given price and hold it till maturity.
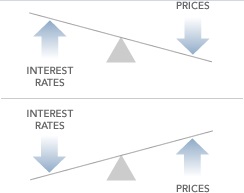
Step III: Understand how interest rates and bond prices move in opposite directions.
As you can see, the yield rises because the bond price has fallen. Or the yield falls because the bond price has risen. There is an inversely proportional relationship between the two. As interest rates go down, bond prices go up (+ve return) and as interest rates go up, prices go down (-ve return).
This inverse relationship is quite intuitive.
Let’s take the above example of a coupon of 5%. When interest rates are trending downwards (say in the region of 4.55%), a bond paying a coupon 5% would be more valuable. As demand for the bond increases, the price of this bond will move higher. The reverse will take place when interest rates increase. This time, bonds with lower coupon become less valuable and so the bond prices fall accordingly.
Step IV: Understand YTM.
YTM is yield to maturity.
YTM is the estimated annual rate of return for a bond assuming that the investor holds the asset until its maturity date and reinvests the payments at the same rate as its current yield.
So it depends on the price you paid when you purchased the bond - if it was on par or at a premium or a discount. The interest you will earn during the balance period. And the assumption that this interest will be reinvested at the same yield. In other words, YTM accounts for the present value of a bond’s future coupon payments. Put together, these are the components of YTM.
The formula for calculating YTM is:
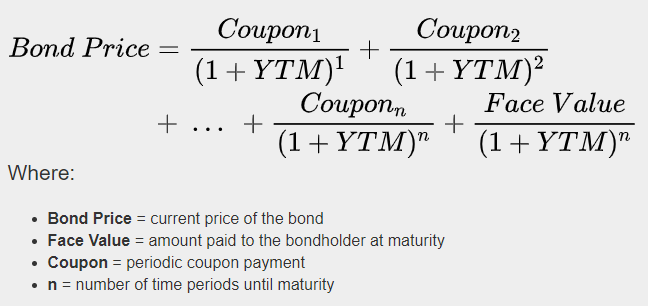
Wrapping it up:
- Return in case of bonds is the combined effect of coupon (interest) rate + capital appreciation.
- As with any instrument traded, the price will rise or fall since the cash flows over the life of this fixed-rate bond are fixed.
- Rising interest rates lower the attractiveness of these fixed cash flows due to the higher discounting rate.
Falling interest rates increase the attractiveness of these fixed cash flows due to the lower discounting rate.
(Discounting rate is the interest rate applied to determine the present value of these cash flows).
- The higher market price of the bond (relative to FV) is the result of an adjustment reflecting lower market interest rates. The lower market price of the bond (relative to FV) is the result of an adjustment reflecting higher market interest rates.
More on Debt Investing
Larissa Fernand is an Investment Specialist and Senior Editor for Morningstar India. You can follow her on Twitter.